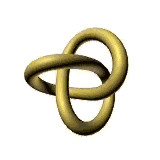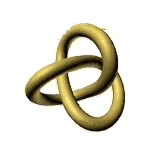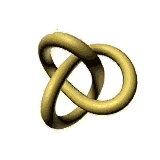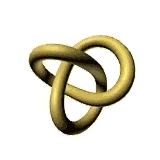
This paper will describe different qualities
that are consistent in equivalent knots. Since the main goal of knot
theory is to prove equivalence between two given knots, the qualities discussed,
called invariants, are very important in knot theory. I will begin
by providing the mathematical definition of a knot, and explaining what
it means for two knots to be equivalent. Then I will proceed into
a discussion of invariants. The paper will conclude with an explanation
of the composition of knots.
![]() Everyone
knows what a knot is in ordinary layman's terms. A piece of string
is knotted if it is twisted around itself in some fashion.
Everyone
knows what a knot is in ordinary layman's terms. A piece of string
is knotted if it is twisted around itself in some fashion.

The mathematical definition is a little more
specific than this. If the knotted piece of string is then taped
together at the two ends, it satisfies the definition of a mathematical
knot. In his paper called "The Theory of Knots", Lee Neuwirth defines
a mathematical knot more precisely: a knot is a one-dimensional closed
curve in three dimensional space without self-intersections.[5] By
closed, we mean that the curve begins and ends at the same point.

The simplest knot is called the unknot, or
the trivial knot. It has no twists or crossings. The unknot can be distorted
deceptively to look like a more complicated knot. UNKNOT
The Unknot
A mathematical definition for equivalence is necessary to begin the description of invariants. Two knots are equivalent when they can be pulled, pushed, stretched, or twisted until they look the same. This intuitive definition will suffice for someone with a limited background in mathematics. However, there is a precise mathematical definition for this. I borrow it from Kunio Murasugi's book, Knot Theory & It's Applications, and include it here.





