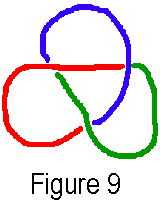
 Another
very interesting invariant of knots is called tricolorability. Adams
writes that a knot has tricolorability when a person can color each strand
of the knot one of three different colors, strands being parts of the rope
that are divided by undercrossings with only overcrossings in between,
and either all three colors or just one color comes together at each crossing.[1]
(see figure 9) To prove that tricolorability is indeed an invariant, we
need only show that every time a Reidemeister move is applied to a tricolored
knot, the tricolorability is maintained. The three moves are applied
in figures 10, 11, and 12, and it is easily observed that the three knots
remain tricolored.
Another
very interesting invariant of knots is called tricolorability. Adams
writes that a knot has tricolorability when a person can color each strand
of the knot one of three different colors, strands being parts of the rope
that are divided by undercrossings with only overcrossings in between,
and either all three colors or just one color comes together at each crossing.[1]
(see figure 9) To prove that tricolorability is indeed an invariant, we
need only show that every time a Reidemeister move is applied to a tricolored
knot, the tricolorability is maintained. The three moves are applied
in figures 10, 11, and 12, and it is easily observed that the three knots
remain tricolored.
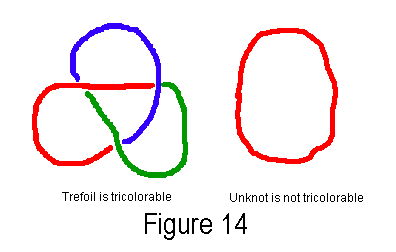
Tricolorability
is a useful invariant because it allows us to prove that there are knots
other than the unknot. This may seem obvious, but we have not proved
it yet. If we can show that the knot called the trefoil knot (see
figure 13) is not the unknot using tricolorability, then we have shown
that there are at least two different kinds of knots, up to deformation.
To show this, see figure 14. In essence, he proved that knots cannot
always be untied without cutting them.
Next Example: The unknotting number





