Is
P
a group under the operation composition of classes? First, we must
define composition of classes. Taking an element from each class,
and joining them by unattaching a strand from each element and joining
the ends composes the elements. Clearly composing two classes [p1] and
[p2] in P
yields a class of paths which is in S
and travels from b to b. (see figure 3)
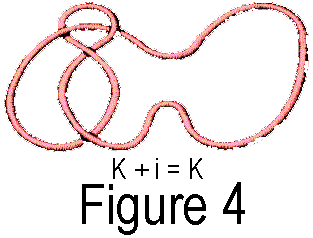Also,
let [i] be the class of paths which never leaves b. Observe that
composing [i] with any class [p] in P
gives the path [p]. (see figure 4)
In addition, note that composition of classes of paths is associative.
Also, for any [p] in P, an element [p]' of P exists for which [p]*[p]' = [i]. In particular, [p]` = [p`], where p` is the inverse of p in P. That is, p*p`=i. We know p` exists, because p` is simply the path p traced in the opposite direction. Notice that for any q in [p], q can be rewritten as p, and hence we can find an element of [p]` that is the inverse of q, namely p`. Therefore, [p]`=[p`].
So we have shown that P is indeed a group under the operation composition of classes of paths.
