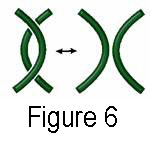
The
second allows the adding or removal of two crossings. (see figure
6)
Another
invariant is the set of Reidemeister moves. Adams describes them
as three moves of the knot which, when applied, maintain the equivalence
of the knot. [1] The first Reidemeister move allows the adding or taking
away of twists in the knot. (see figure 5)
The
second allows the adding or removal of two crossings. (see figure
6)
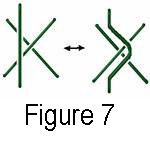The
third allows the sliding of a strand of the knot from one side of a crossing
to the other side of the crossing. (see figure 7)
It can clearly be seen that these moves maintain equivalence between knots. The Reidemeister moves do in fact completely characterize knots. That is, if the Reidemeister moves are applied to one knot a finite number of times to get another knot, then the two knots are equivalent. This is proved in Gerhard Burde and Heiner Zeischang's book entitled Knots, and I will not show it here.[2]
Next Example: Tricolorability
